写在前面
突然发现本鸽子已经四个月没写什么像样的技术文章了,因为还在上学,这个学期的学习压力实在有点大( 老ddl战神了)。所以只能先把博客先鸽了。╮(╯▽╰)╭
不过这个学期还是学到了很多东西的,现在期末考试完,也稍微有了一点闲暇时间,可以来记录一下这个学期的收获。o( ̄▽ ̄)ブ
这次得的是一等奖第一名,感谢队友的辛勤努力,希望再接再厉。(ง •_•)ง
题目分析

- 由于单片机的ADC只能采集0-3.3V的电压,所以需要经过前级调理电路把电压转换到0-3.3V。
- 根据题目发挥部分的要求,最大电压为2.5+5=7.5V(5V直流偏置加5V峰峰值),最小电压为-2.5V(5V峰峰值)
所以硬件采用的方案是电平搬移+衰减,先将整体电平抬高到0V之上,然后经过衰减得到0-3.3V的电平。
在这个过程中需要保持电平的线性关系。这就要求需要在测量边界处留出一些余量。 - 频率采用单片机的输入捕获,最高可以做到1MHz。
- 峰峰值的测量使用ADC找最值的方法,而不是峰值检波电路。
- 波形的判断采用波形因数法,计算速度快,调参后准确率高。
ADC采样简介
根据ST官方手册,STM32是逐次比较型ADC,其基本原理简单来说是让信号电平给一个电容序列充电,然后把获得的充电电压依次与1/2参考电压,3/4参考电压….比较,最后将结果输出。
下面是基本原理图。
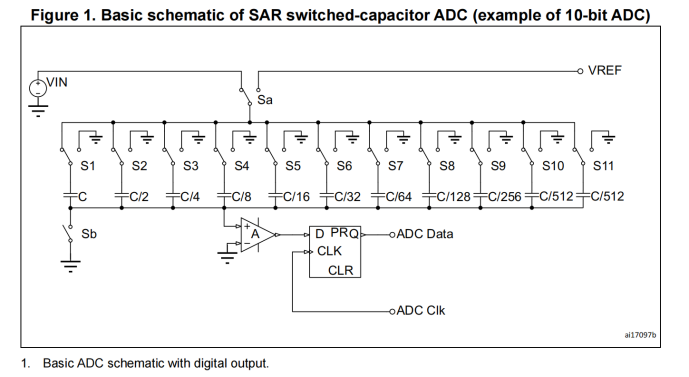
一次采集电压由两个过程组成,采样和转换。
采样时间指的是把电容从零充电到信号电平所需要的时间,转换时间指的是内部的开关序列将参考电压通过二分法逼近到信号电压所需要的时间。
所以ADC采样率由下面这个式子给出
ADC采样率 = ADC主频 / (采样时间 + 转换时间)
ADC主频取决于时钟域的来源与分频,H7系列最高不能超过36MHz,F1系列最高不能超过14Mhz。
采样时间由用户设定,可以有以下几种
转换时间取决于ADC分辨率,可以有以下几种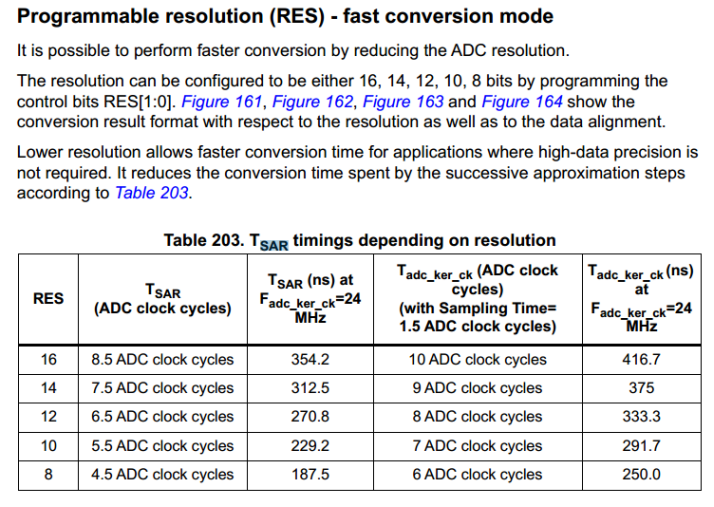
根据上文,STM32H743在16位下,最高采样速率可以达到3.6M每秒,36/(1.5+8.5)=3.6。
但是需要注意,最大速率下的ADC不一定稳定,最大能稳定的采样速率还跟芯片的封装有关,如下表所示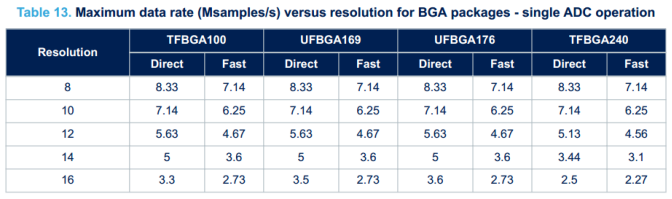
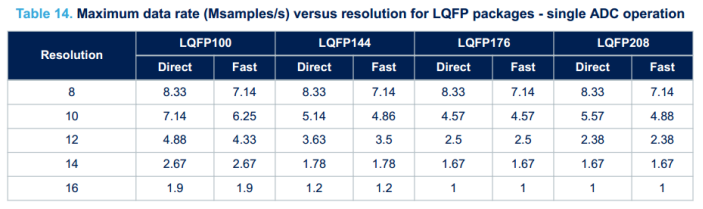
其中BGA封装在高分辨率的情况下最大速度远远大于LQFP封装。
过采样
过采样是多次采样求平均值。比如过采样设置4,那么将采集4个值进行累加。接着配置右移动2位的话,相当于将刚才的累加值除以4,得到平均值。
这样就不需要在程序里求平均了,非常适合采样稳定度要求高,而速率要求没那么高的场合。
而过采样还有一种用法就是牺牲采样速率提高采样精度,根据过采样技术,每提高1位ADC分辨率,需要增加4倍的采样率。比如G0系列过采样设置256,右移4位,相当于在12位ADC的基础上又获得了4位精度,可以当作16位ADC来使用。
这里我开启的是四倍过采样求平均,效果很好,对于最大值和最小值的捕捉非常准确。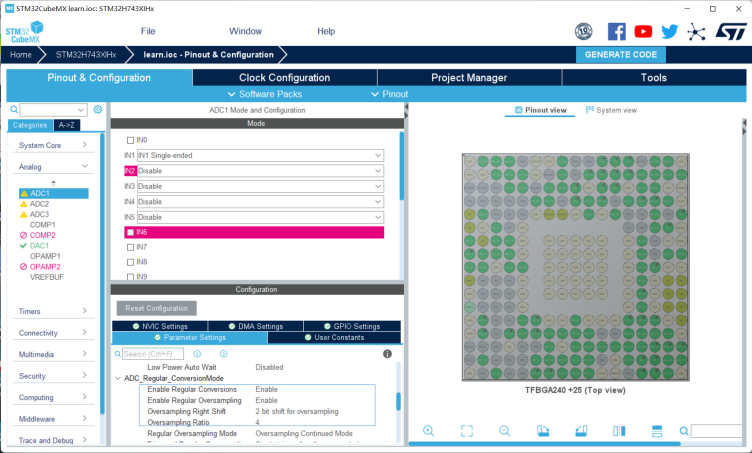
这里我做了一个取舍,使用的是14位分辨率,采样速率能到4M每秒,4倍过采样,相当于1M采样率。
最值计算
将采样数组进行排序,这里使用的是冒泡排序,时间复杂度为O(n^2)。
取最大的1%进行平均,获得最大值。最小值同理。
全部求和并除以长度,获得均值。
/*计算并显示最大最小值峰峰值*/
void Dis_MaxMinVpp(unsigned int *Original, int N, int type)
{
unsigned short Array[Sampling_CNT]; // 用临时数组排序,避免改变原数组
for(int i=0;i<N;i++)
Array[i] = Original[i];
for(int i=0;i<N;i++) // 从小到大排序
for(int j=i+1;j<Sampling_CNT;j++)
if(Array[i] > Array[j])
{
unsigned short temp;
temp = Array[i];
Array[i] = Array[j];
Array[j] = temp;
}
unsigned short max, min;
if(type == Sin||type == Triangle||type == 0) // 如果是正弦或者三角波,仅取1%的最值点进行均值处理,防止拉低幅值过多
{
long long sumofmax=0,sumofmin=0;
int cnt = Sampling_CNT/100;
for(int i=0;i<cnt;i++)
{
sumofmin += Array[i];
sumofmax += Array[Sampling_CNT-1-i];
}
max = sumofmax/cnt;
min = sumofmin/cnt;
}
else if(type == Square) // 如果方波,可以取5%点进行均值处理
{
long long sumofmax=0,sumofmin=0;
int cnt = Sampling_CNT/20;
for(int i=0;i<cnt;i++)
{
sumofmin += Array[i];
sumofmax += Array[Sampling_CNT-1-i];
}
max = sumofmax/(cnt);
min = sumofmin/(cnt);
}
Global_ADCMax = max;
Global_ADCMin = min;
}输入捕获
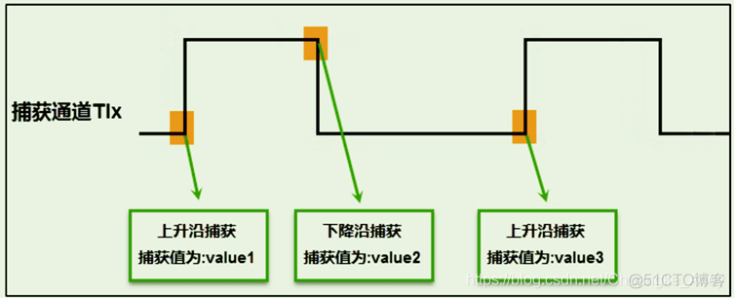
输入捕获的原理是通过检测IO电平的上升沿和下降沿来获取高电平时间和低电平时间,通过时间来计算周期和占空比。
在第一次上升沿处记录时间A,第一次下降沿记录时间B,第二次上升沿记录时间C
那么周期就是C-A,高电平时间为B-A
/*Main函数里的输入捕获处理 计算频率*/
void InputCaptureProcess()
{
switch (capture_Cnt) // 输入捕获
{
case 0:
capture_Cnt++;
__HAL_TIM_SET_CAPTUREPOLARITY(&htim5, TIM_CHANNEL_1, TIM_INPUTCHANNELPOLARITY_RISING);
HAL_TIM_IC_Start_IT(&htim5, TIM_CHANNEL_1);
break;
case 4:
high_time = capture_Buf[1] - capture_Buf[0];
all_time = capture_Buf[2] - capture_Buf[1];
uint32_t high_ns = high_time * 5;
uint32_t all_ns = all_time * 5;
if(all_ns> high_ns)
Global_duty = ((double)high_ns+5)/all_ns*100; // 计算占空比
else
Global_duty = (((double)high_ns - all_ns)-5)/all_ns*100;
sprintf(String_lcd,"Period:%d ns", all_ns+5); // 显示周期
LCD_DispStr(20,30, " ", &tFont16);
LCD_DispStr(20,30, String_lcd, &tFont16);
sprintf(String_lcd,"Duty %3.1lf %%", Global_duty); // 显示占空比
LCD_DispStr(20,45, " ", &tFont16);
LCD_DispStr(20,45, String_lcd, &tFont16);
Global_Fre = 1.0/((double)(all_ns)/1000000000); // 计算频率
Dis_Fre(Global_Fre); // 显示频率
__HAL_TIM_SET_COUNTER(&htim5, 0);
capture_Cnt = 0;
break;
}
}
/*输入捕获的中断处理*/
void HAL_TIM_IC_CaptureCallback(TIM_HandleTypeDef *htim)
{
if(TIM5 == htim->Instance) // 输入捕获
{
switch(capture_Cnt)
{
case 1:
capture_Buf[0] = HAL_TIM_ReadCapturedValue(&htim5,TIM_CHANNEL_1);//获取当前的捕获值.
__HAL_TIM_SET_CAPTUREPOLARITY(&htim5,TIM_CHANNEL_1,TIM_ICPOLARITY_FALLING); //设置为下降沿捕获
capture_Cnt++;
break;
case 2:
capture_Buf[1] = HAL_TIM_ReadCapturedValue(&htim5,TIM_CHANNEL_1);//获取当前的捕获值.
__HAL_TIM_SET_CAPTUREPOLARITY(&htim5,TIM_CHANNEL_1,TIM_ICPOLARITY_FALLING); //设置为上升沿捕获
capture_Cnt++;
break;
case 3:
capture_Buf[2] = HAL_TIM_ReadCapturedValue(&htim5,TIM_CHANNEL_1);//获取当前的捕获值.
HAL_TIM_IC_Stop_IT(&htim5,TIM_CHANNEL_1); //停止捕获 或者: __HAL_TIM_DISABLE(&htim5);
capture_Cnt++;
}
}
}波形判断
有很多种判断波形的方法,FFT获得谐波分量,求导判断突变点,我在这里使用的是波形因数法。本质上是对面积进行积分,利用不同形状的波形的占比不同来判断。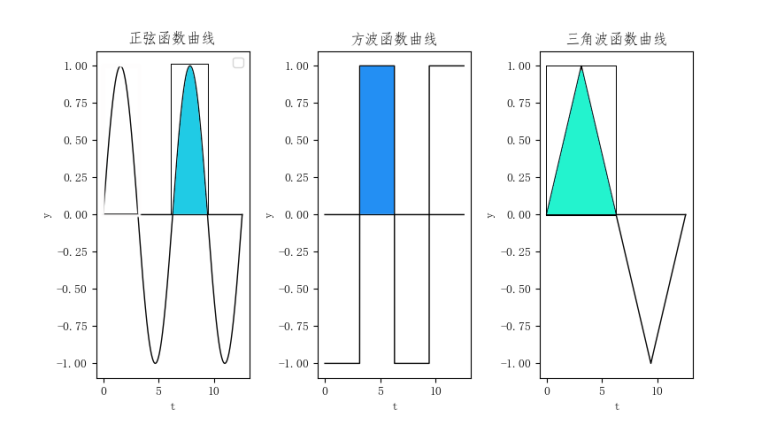
波形因数法的原理是不同波形的波形因数不同,即图中颜色区域的面积与矩形的占比。理论值正弦波0.707,方波1,三角波0.5
实际上计算结果不一定接近理论值,但一定为方波最大,正弦波其次,三角波最小。
而且不同采样率也会影响计算出的值,需要通过测试来确定三种波形的阈值。
代码编写的原理是,先找到均值的跳变点,即左端小于均值,右端大于均值,即认为是左点。右点同理,然后再归一化计算矩形系数。
/*波形判断函数 变量为buffer数组,数组个数,数组最大最小值*/
int WaveTypeJudge(unsigned int *Wave_Buffer,int N, int max, int min)
{
int vpp = max - min, mid = (max + min)/2;
printf("mid %.3lf\n", mid*3.3/16384);
int mark1, mark2, gap;
for(int i=0;i<Sampling_CNT-1;i++)
{
if( Wave_Buffer[i]<mid && Wave_Buffer[i+1] >mid ) // 跳变点1
{
mark1 = i+1;
break;
}
}
if(mark1<0 || mark1>Sampling_CNT-1)
mark1 = 0;
printf("Mark1 %d\n", mark1);
for(int i=mark1+1;i<Sampling_CNT-1;i++) // 跳变点2
{
if(Wave_Buffer[i]>mid && Wave_Buffer[i+1] <mid )
{
mark2 = i;
break;
}
}
if(mark2<0 || mark2>Sampling_CNT-1)
mark2 = 0;
printf("Mark2 %d\n", mark2);
gap = mark2 - mark1;
printf("gap %d mark1 value:%.3lf mark2 value:%.3lf\n",gap, Wave_Buffer[mark1]*3.3/16384, Wave_Buffer[mark2]*3.3/16384);
double D[Sampling_CNT]; // 归一化数组
for(int i=mark1;i<=mark2;i++) // 归一化
{
D[i] = (1.0*Wave_Buffer[i]-min)/vpp;
}
double sum=0;
for(int i=mark1;i<mark2;i++)
{
sum += D[i];
}
sum = sum/(mark2-mark1+1); // 计算矩形系数
printf("Area %.3lf", sum);
int type=0;
if(sum > 0.85)
type = Square;
else if (sum > 0.755 && sum <0.85)
type = Sin;
else if (sum < 0.760 && sum >0.701)
type = Triangle;
Global_Type = type;
Dis_Type(type); // 显示波形种类
return type;
}波形显示
波形显示就是把ADC采集到的电压数据依次绘制到屏幕上。这样在屏幕上看到的就是信号随时间的变化,也就是波形。
这里波形显示原理与真正的示波器原理类似但不完全相同,真正的示波器有存储显示,抹迹显示还有卷动显示等方式。
在这里只需要采集并显示即可,也就是存储显示。
确定绘制起始点
因为每次采样并不一定能从波形的起始点开始,所以需要对采集得到的波形数组处理进行一定的处理。
比如下图就是将波形从均值处截取。把之前的数据丢弃,将截取后的数组显示在屏幕上。这样每次观察到的波形就是一样的。
这其实就是示波器的触发值的设置,这里采用的是均值上升沿触发。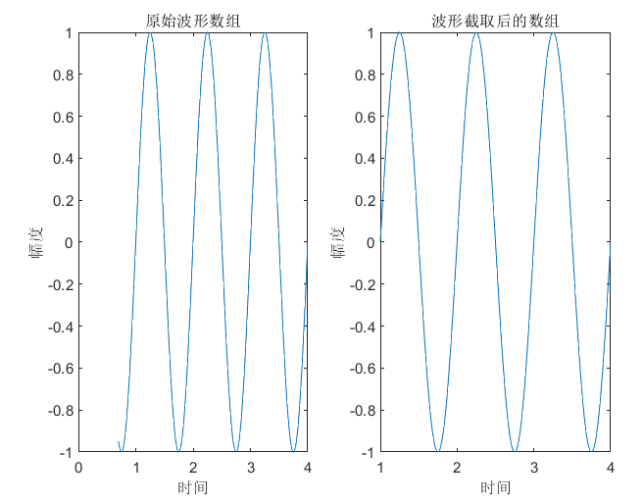
幅值与坐标对应关系
首先需要在屏幕上划分一块显示波形的区域,如X轴0-800,y轴150-450这一块区域作为显示区域。
对于一个采集到的连续的波形数组来说,数组的下标对应着时间,数组的每一个值都对应着一个幅值。
所以可以获得这样一个关系:
X[i] = 数组下标i / X轴缩放倍数 + X轴偏移
Y[i] = (数组值i-均值)×Y轴缩放倍数 + Y轴平均值(300) + Y轴偏移
在这里,采样数组是一个长度恰好为800的数组,所以不需要经过X轴的缩放,也方便了代码的理解和编写。
/*波形重排显示 变量为存储波形的数组,数组大小,数组最大值,数组最小值*/
void Wave_Display(unsigned int *Wave_Buffer, int N, int max, int min)
{
int vpp = max - min, mid = (max + min)/2;
printf("mid %.3lf\n", mid*3.3/16384);
double mvmid = mid*3300.0/16384; // 中值点
int mark1, mark2;
for(int i=0;i<Sampling_CNT-1;i++)
{
if( Wave_Buffer[i]<mid && Wave_Buffer[i+1] > mid ) // 上升沿跳变点1
{
mark1 = i+1;
break;
}
}
if(mark1<0 || mark1>=Sampling_CNT-1)
mark1 = 0;
printf("Rising Mark1 %d\n", mark1);
for(int i=mark1+1;i<Sampling_CNT-1;i++) // 上升沿跳变点2
{
if(Wave_Buffer[i]<mid && Wave_Buffer[i+1] > mid )
{
mark2 = i;
break;
}
}
if(mark2<0 || mark2>=Sampling_CNT-1)
mark2 = 0;
printf("Rising Mark2 %d\n", mark2);
int gap = mark2 - mark1;
if(gap < 0)
gap = 0;
printf("Gap %d\n", gap);
unsigned short Y[Sampling_CNT]; // 电压,单位mV
unsigned short X[800]; // X轴坐标点 0-799
for(int i=0;i<800;i++) // 将X轴坐标点置为0~799
{
X[i] = i;
}
for(int i=0;i<Sampling_CNT;i++) // 将Y轴坐标点置为中间值
{
Y[i] = mvmid;
}
if(gap != 0) // 若采集到的波形有一个完整周期就绘制
{
for(int i=0;i<Sampling_CNT-mark1-1;i++) // 换算成真实值
{
Y[i] = Wave_Buffer[i+mark1]*3300.0/16384;
}
for(int i=0;i<Sampling_CNT-mark1;i++) // 计算Y轴坐标
{
Y[i] = 300 - (Y[i*5]-mvmid)/10;
}
for(int i=Sampling_CNT-mark1;i<800;i++) // 未经过处理的置为中间值
{
Y[i] = 300;
}
for(int i=0;i<800;i++) // 将超限的Y轴置为最大或最小
{
if(Y[i]<150)
Y[i]=150;
if(Y[i]>450)
Y[i]=450;
}
for(int i=0;i<(Sampling_CNT-mark1)/5-1;i++) // 绘制波形
{
LCD_DrawLine(X[i], Y[i],X[i+1], Y[i+1],CL_YELLOW);
}
}波形内插
在信号频率很高的情况下,一个周期的采样点数很少,此时若用直线去连接这些点,恢复出来的波形和原始波形的差距就会比较大。
我们可以使用波形内插的方法来缓解这个问题,有多种内插方式,对于信号波形来说,一般使用的是sinc插值。
这里是一个Matlab的测试案例,使用sinc插值之后,可以看到恢复出的信号非常接近原始信号。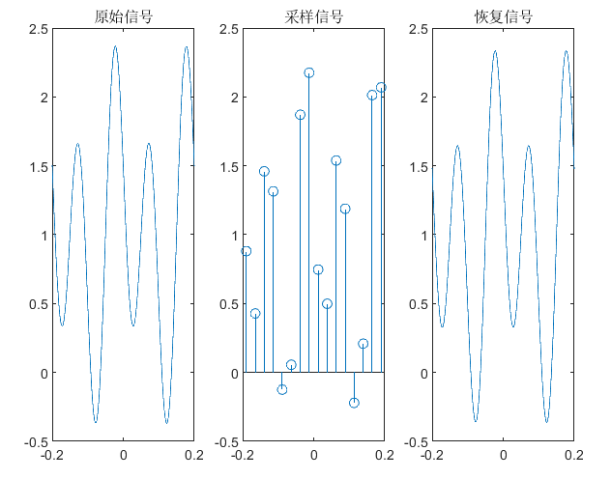
%参数设定
T = 2;
f1 = 5;
f2 = 10;
fs = 40;
%可得参数
N = T * fs;
t = linspace(-T/2, T/2, 100*N);
f_ori = 0.5 * cos(2 * pi * f1 * t) - sin(2 * pi * f2 * t) + 1;
figure(1);
subplot(1,3,1)
plot(t, f_ori);xlim([-T/10, T/10]);title('原始信号');
%采样
t2 = linspace(-T/2, T/2, N);
f_sam = 0.5 * cos(2 * pi * f1 * t2) - sin(2 * pi * f2 * t2) + 1;
subplot(1,3,2)
stem(t2, f_sam);xlim([-T/10, T/10]);title('采样信号');
%恢复
y = [];
for i = 1 : length(t)
x = t(i);
h = sinc((x - t2).*fs);
g = dot(f_sam, h);
y = [y,g];
end
subplot(1,3,3)
plot(t, y);xlim([-T/10, T/10]);title('恢复信号');用C语言重构上述代码,方便移植到嵌入式设备上。
#include <stdio.h>
double sinc(double i)
{
return i ? sin(3.1415926535 * i) / (3.1415926535 * i) : 1;
}
/* x为采样数组,size为数组大小,d为目标插值,可以为小数*/
double get_interpolate(double x[], int size, double d)
{
int i;
double sum = 0;
for (i = 0; i < size; i++)
sum += x[i] * sinc(d - i);
return sum;
}
/* x为采样数组,size为数组大小 X为插值后的数组,targetsize为插值后数组的大小*/
double sinc_interpolate(double x[], int size, double *X, int targetsize)
{
for (int i = 1; i <= targetsize; i++)
{
X[i] = get_interpolate(x, size, 1.0 * (i - 1) * size / targetsize);
printf("%lf\n", X[i]);
}
}
int main()
{
double f_sample[80] = {1.50000000000000, 0.350218707514647, 1.02981542126440, 1.63428203159719, 0.420945134414632, -0.330611364701946, 1.14882575438682, 2.36761177655162, 1.34002139510013, 0.336515950817689, 1.14790049772393, 1.58614766032644, 0.267209524616113, -0.271815798463299, 1.34415553674556, 2.35800974404114, 1.18089106394594, 0.345632700390290, 1.26131189972505, 1.51583139142586, 0.122580141947042, -0.186681197435368, 1.53210855046169, 2.32173054166489, 1.02653738079722, 0.376742548729278, 1.36644087239649, 1.42466154335987, -0.00917203061633165, -0.0767431568445289, 1.70867956548973, 2.26011289857373, 0.880709036892182, 0.428429189646382, 1.45989843638453, 1.31454247186115, -0.124542498404740, 0.0558690778948849, 1.87013775734842, 2.17508452646085, 0.746881328267354, 0.498726167175591, 1.53860560129212, 1.18790900013601, -0.220382865526669, 0.208482285063405, 2.01311630856953, 2.06911109483560, 0.628169714175406, 0.585170708848189, 1.59987565541602, 1.04766712628891, -0.293981817799452, 0.377942495163037, 2.13469293037414, 1.94513195924319, 0.527252820426470, 0.684870257644629, 1.64148642527270, 0.897122491248322, -0.343135423968915, 0.560690204597402, 2.23245929983456, 1.80648427799040, 0.446306821229624, 0.794579995243510, 1.66174065245278, 0.739898401681914, -0.366204968511657, 0.752845703368009, 2.30457768677453, 1.65681744391457, 0.386952843606612, 0.910789370783001, 1.65951293634291, 0.579845468358066, -0.362160841966680, 0.950302391070532, 2.34982336705478, 1.50000000000000}; // 采样数组
double f_restore[800]; // 恢复后的数组
sinc_interpolate(f_sample, 80, &f_restore, 800);
return 0;
}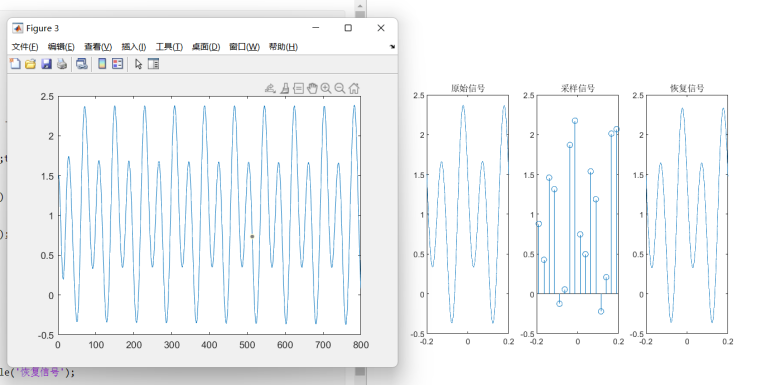
这个C语言测试案例是将一个80个点的离散信号通过内插恢复到800个点,然后将800点输入matlab并绘图,和原图比较,发现非常接近原始波形。
一些照片
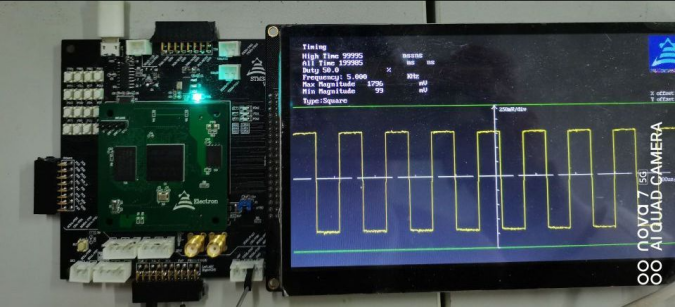
结语
这篇文档算是对本次比赛中所用的技术的一个整理,方便自己日后复盘调用,也旨在用通俗易懂的方式给后来人讲解清楚一些技术的原理和应用方法。
希望能有所帮助。
参考链接
STM32ADC https://blog.csdn.net/wallace89/article/details/117048846
Matlab内插 https://blog.csdn.net/Differoucius/article/details/121142456