写在前面
这次省赛的成绩还没出来,但是可以预见的是不会太好,至少没有达到我们队伍的预期,其原因不适合在博客上写出,有方案选择的原因,也有评审时的意外因素。
通过这次比赛,算是得到了一个教训,不能顾此失彼,要先完成基础部分再去考虑扩展部分。
作为软件队员,在此记录一下所使用到的思路和算法。
题目分析

题目的输入信号有100mv,属于一个比较大的信号,从信号源直出,通过SMA线输入,信号信噪比非常高,所以不需要考虑信号在传输过程中被干扰。
基本要求的情况下载波频率10MHz,提高要求到了30Mz,在实际通信中不算太高,但早已超过单片机ADC或者普通外挂ADC的最高采样速率,如果要直接采样只能采用FPGA驱动的并行ADC模块。
但是我目前并不会FPGA,所以只能考虑别的方案。比如常见的通过本振+混频器降频到一个较低的频率。
要计算调幅度Ma,这就要求获得调制后信号的频谱,也就是要做FFT。这就要求ADC的采样频率能够高于中心频点+最大频偏之和的两倍。
要计算调频度Mf和最大频偏Δf,同上,还涉及到一些算法的问题,在后面详细讨论。
提高要求需要我们自动识别出载波频率,也就是本振源频率可以通过数字方式调整,扫频到载波频点。
要识别信号的调制方式,通过分析频谱谱线的条数可以获得,但是有一些情况下,AM的频谱非常接近FM的频谱,这个在后面详细讨论。
系统架构
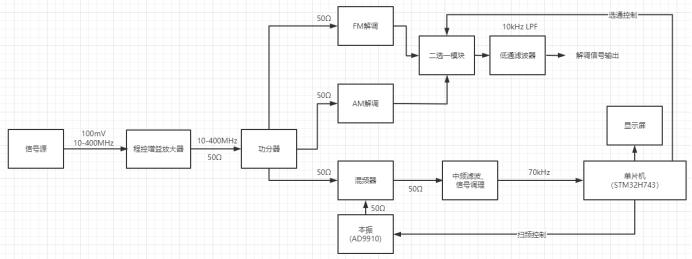
综合前面的分析,本项目的系统框图如图 1 所示。该系统由程控增益放大器、功分器、FM 解调模块、AM 解调模块、本振源、混频器、中频滤波器、信号调理模块、低通滤波器和单片机等几部分组成。
被测信号首先通过0~30dB可调的程控增益放大器放大,再通过功分器后同时送往 AM 解调、FM 解调和混频器。
AM 解调和 FM 解调模块完成对应的解调功能,并通过二选一开关及低通滤波器后输出解调结果。
单片机控制 AD9910本振输出并送往混频器,由混频器完成对被测信号的混频。混频的输出通过中频滤波和信号调理电路后,得到 70kHz 的中频信号。
单片机对该 70kHz 中频信号进行采集、FFT 运算和数字信号处理,识别出调制信号的载波频率、调制信号频率、调制参数等信息,并控制LCD屏幕显示相应信息。
软件部分
这一部分偏实践,会有比较多的实际代码,我会用图片与文字的结合方式,尽量讲解清楚。
ADC+DMA
为了保证采样速率和采样间隔的一致性,需要使用ADC定时器中断+DMA的方式来做采样。
ARM官方的DSP库最大支持4096个点,要做到200Hz分辨率的话,要达到200*4096=819.2K每秒的采样率。这个H7还是完全可以做到的。
ADC设置,异步时钟二分频,64/2=32MHz,在H7系列的ADC最大稳定时钟频率36MHz之内。
数据管理模式设置为DMA One Shot Mode,而不是存储在DR寄存器或者DMA循环模式,便于我们一次采集4096个点。
触发源设置成Timer6 Trigger Out Event,用定时器更新来触发采样,然后用DMA传输到内存数组钟,直到存满4096个点。
其他的按照图中的设置来。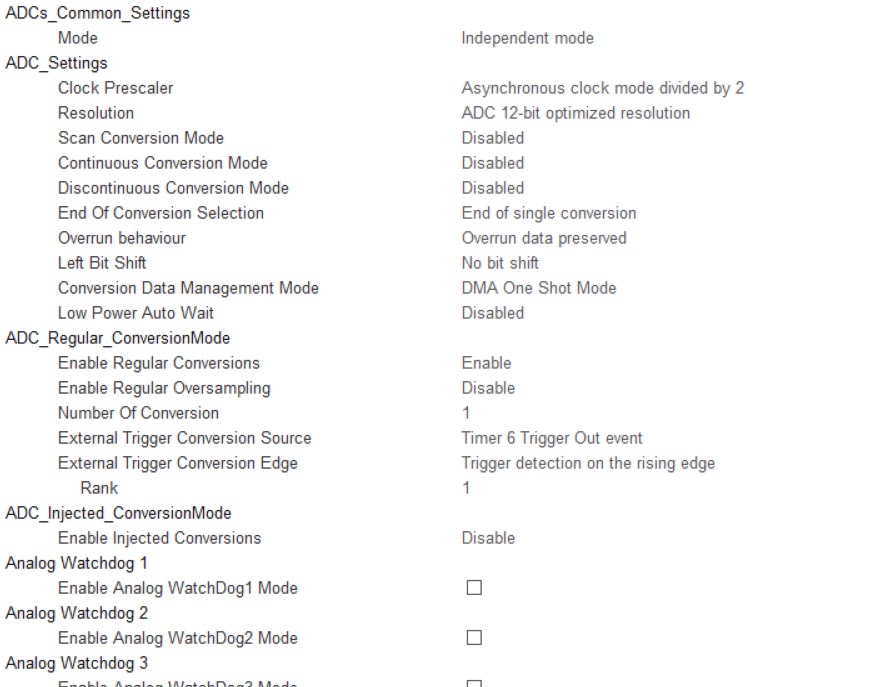
定时器设置,定时器主频200MHz,在这个设置下是819.7KHz采样率,并不完全是819.2KHz,所以需要一些调节的方式,在后面会讲到。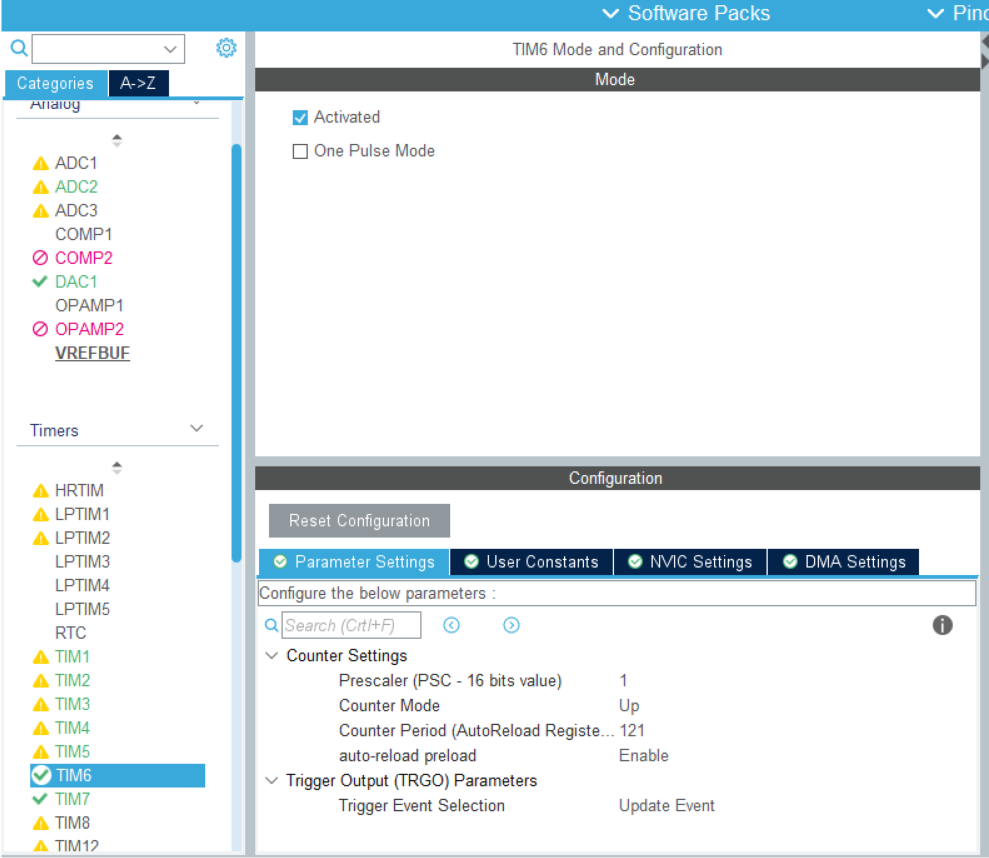
DMA设置,传输字长半字,Normal模式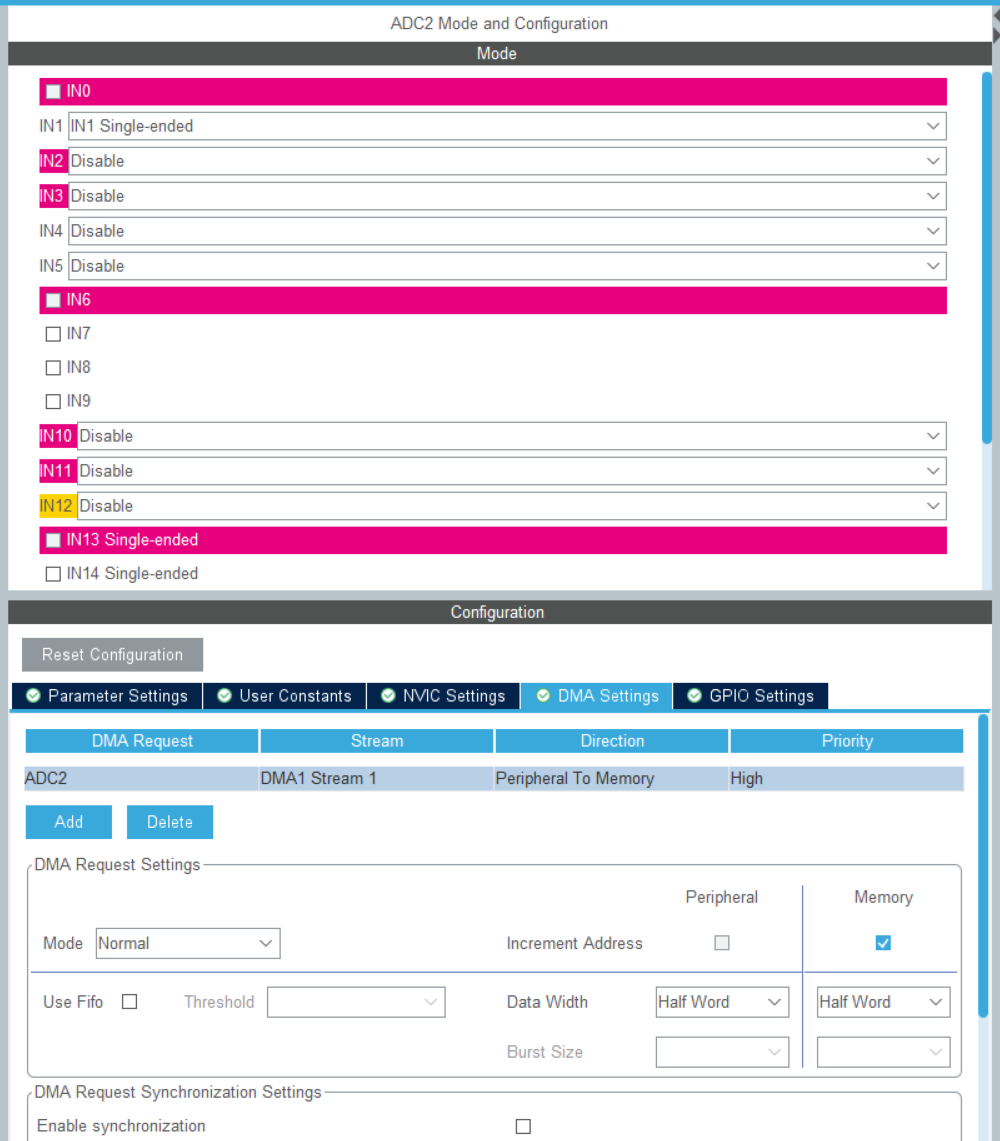
FFT
根据MCU的内核型号和是否有FPU单元添加特定的lib,lib已经打包上传。
地址 https://www.aliyundrive.com/s/Lc1atnFUEgf
提取码: 1y9p
下载后把后缀改成.zip就可以了。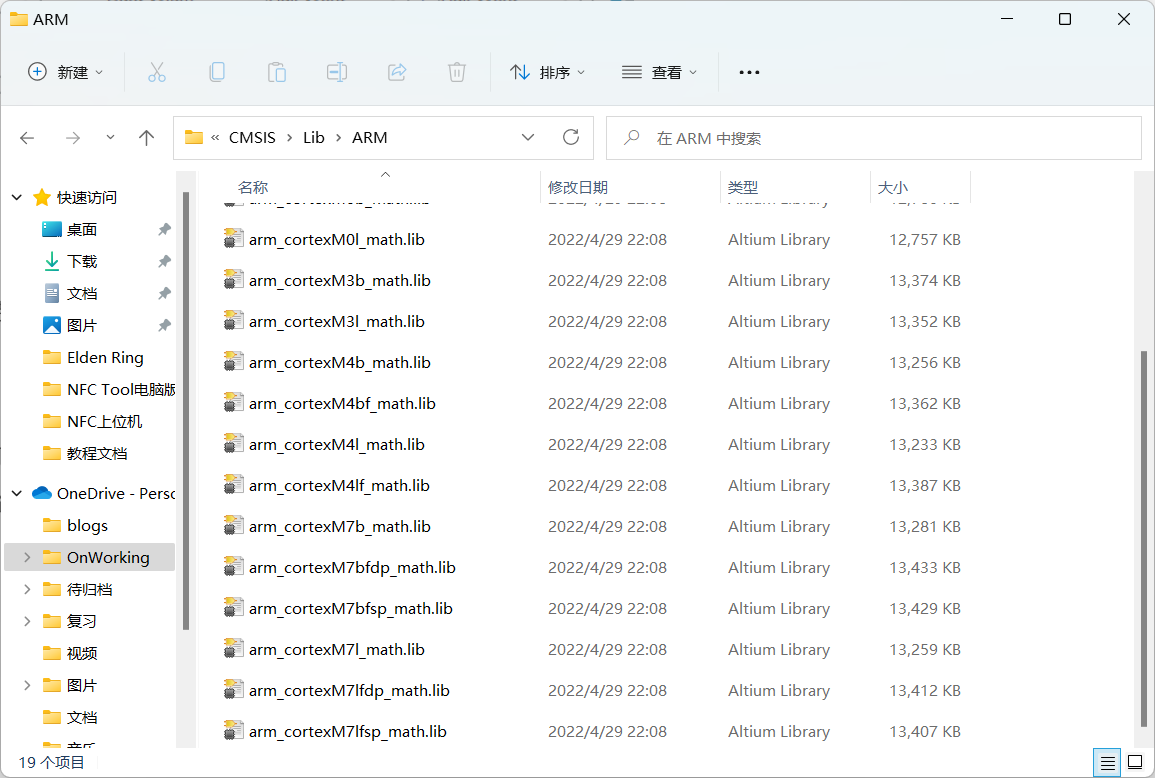
M0、M3、M4、M7分别代表Cortex-M0、Cortex-M3、Cortex-M4、Cortex-M7内核上运行的库;
字母l代表小端地址格式,b代表大端地址格式(所有STM32皆为小端地址格式处理器);
字母f代表使用浮点处理单元(FPU)进行计算的库。
字母dp表示fpu是双精度的,sp表示fpu是单精度的。
例如,我使用的H743是M7内核,有双精度FPU,小端。所以选择M7lfdp
ADC+FFT的代码
/* ADC采样并做FFT 结果放在全局数组fft_outputbuf中 */
void Sample_FFT(int debug, int serialplot)
{
HAL_TIM_Base_Start(&htim6);
HAL_ADC_Start_DMA(&hadc2, (unsigned int*)Global_ADC_buffer, Sampling_CNT); // 开启ADC并等待一段时间,ADC结果存在Global_ADC_buffer全局数组中
HAL_Delay(10);
HAL_TIM_Base_Stop(&htim6);
HAL_ADC_Stop_DMA(&hadc2);
for(int i=0;i < FFT_LENGTH;i++)
{
fft_inputbuf[i*2] = Global_ADC_buffer[i]*3300/4096 ; // 按手册要求的实部虚部交替的方法填充数组
fft_inputbuf[2*i +1] = 0;
}
arm_cfft_f32(&arm_cfft_sR_f32_len4096,fft_inputbuf,0,1); // 执行FFT变换,arm_cfft_sR_f32_len4096为宏,定义旋转因子
arm_cmplx_mag_f32(fft_inputbuf,fft_outputbuf,FFT_LENGTH); // 把运算结果复数求模得幅值
if(debug == 1)
for(int i=50;i <= 650;i++) // 是否打印FFT每个频点的幅值信息
printf("%.1lf KHz Mag %.3f\n", 200.0*i/1000, fft_outputbuf[i] );
if(serialplot == 1)
for(int i=40;i <= 650;i++) // 是否打印到SerialPlot
printf("%.3f\n", fft_outputbuf[i] );
}扫频算法*
由于前面说的,实际采样率是819.7KHz,这会让第3500个点的70KHz频率偏移到70.04KHz,由于我们频率分辨率只有200Hz,也就是0.2KHz。
所以这个频点上的幅值会被分散到70.0KHz和70.2KHz上,虽然是70.0KHz分走了大部分,但是也有一部分被分到了70.2KHz,会影响后续的计算。
于是我们干脆一不做二不休,微调DDS的频率使得中心频率为70.0KHz。
扫频法找载波频率的理论很简单,就是改变DDS本振的频率,看70KHz这个中频上有无一个很大的幅值。
因为无论是AM,FM,还是未调制的信号,在基频上总有一个频点, 通过混频器降到低频后,也一定有个频点。
那么该怎么通过FFT的结果认定70.0KHz处有频点呢,我这里采用的判断条件是,如果这个点的幅值大于左右相邻的点,且幅值大于平均值的五倍,就认为这个点是频点。
但是,万事都没这么完美,由于镜像频率的存在(暂且这么称呼),会出现误判断的情况。
举个例子,在载波基频为10MHz的时候,用9.93MHz的本振频率去扫,可以获得70KHz和19.93MHz的两个频率,此时19.93MHz的频率是无法通过低通滤波器的。
所以只留下了我们需要的70KHz。
但是由于10MHz的DDS会在20MHz产生一个谐波。如果用19.93MHz的DDS去扫,会得到70KHz和29.93MHz两个频率,也是能满足以上的判断条件的。
在这里简单解释一下产生谐波的原因, DDS或者说DAC的直接输出是一个阶梯波,就是一个正弦波乘上冲激函数,但是由于非理想冲激函数的宽度不为0,导致产生的信号在频谱上就是按照倍频延拓,包络是sinc。(感谢群友CNPP的解释),下图是为什么阶梯波的频域波形是这样的示意图。
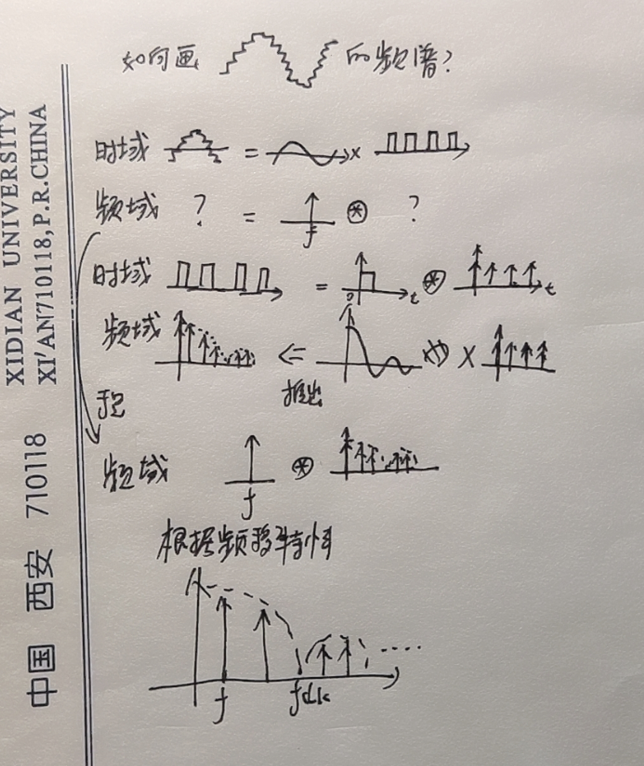
ADI的DDS应用手册也向我们指出了这一点。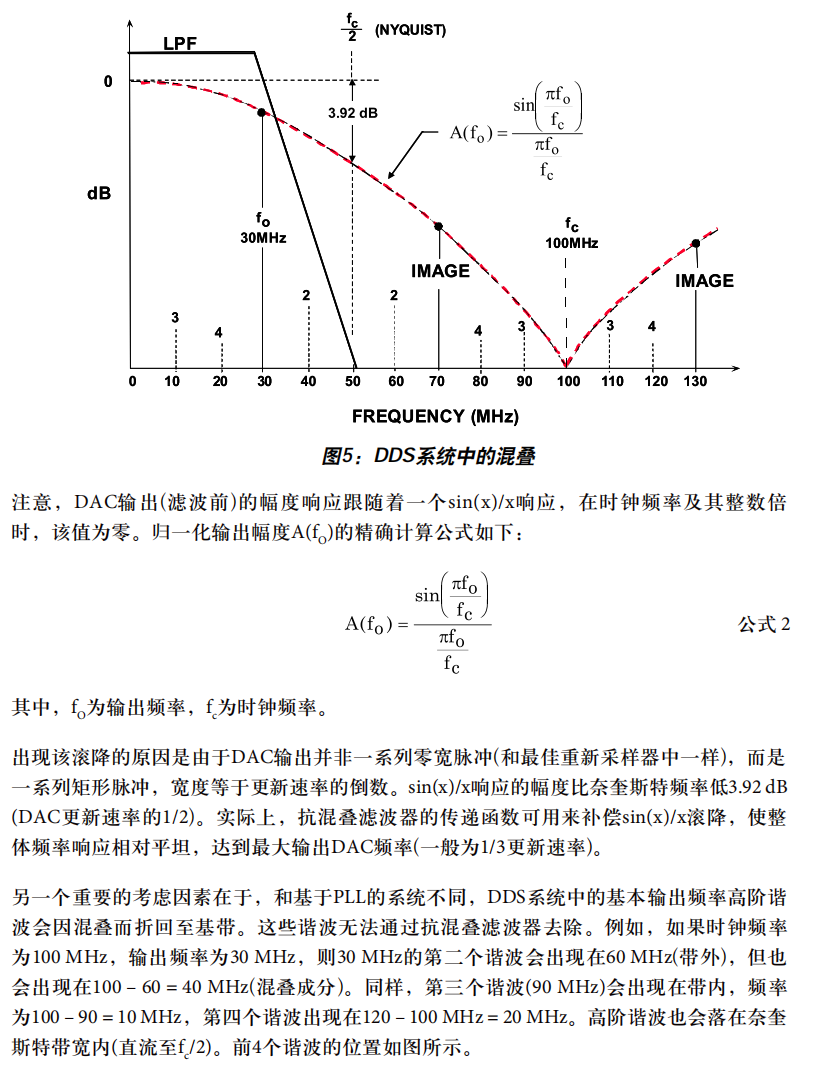
修正后的判断方法*
所以我们还得修正判断方法,我采用的是70.0KHz频率处的信噪比+频点个数综合判断的方法。
具体来说就是算出70.0KHz频率处的信噪比,乘以某个系数a作为置信度A,
数出10KHz-130KHz区间内的频点数,乘以某个系数b作为置信度B。
然后将置信度A+置信度B的和作为Possibility,一轮扫频下来,每个频点都有一个Possibility。
取最大的一个Possibility,就是我们的载波频率。
这样方法的基本原理是,由于高次谐波下幅值会衰减 ,所以信噪比和频点数会降低。所以最大的Possibility就是真正的载波频率。
但是应该还有更好的算法,欢迎讨论。
下面是具体实现的代码。
// 控制扫频上限 SIZE (X-10)*2 + 1
#define SIZE 41
#define UPFRE 30000000
/* 自动扫频并锁定频率,返回值为锁定的频率 */
int LockOn()
{
int sweepfre=9929900;
double RatioArray[SIZE] = {0};
int index=0;
double Possibilities[SIZE] = {0};
int k=0;
while(isLocked != 1)
{
int SumofOverOne = 0;
#define TIMES 10
double sumofRatio = 0;
int BigPoint=0;
Freq_Amp_set(sweepfre, 600);
printf("Sweep Fre %.1lf MHz...",(sweepfre+70000.0)/1000000);
for(int i=0;i<TIMES;i++)
{
HAL_Delay(1);
Sample_FFT(0, 0);
double sumof = 0;
for(int i=50;i <= 650;i++)
sumof += fft_outputbuf[i];
double avg_mag = sumof / 600 ; // 求出平均值
for(int i=50;i<650;i++)
{
if(fft_outputbuf[i]/avg_mag > 20 )
BigPoint++;
}
SumofOverOne += BigPoint;
int k=352; // 算中心频点与周围的信噪比
double Ratio = (fft_outputbuf[k]+fft_outputbuf[k+1]+fft_outputbuf[k-1])/((fft_outputbuf[k-4]+fft_outputbuf[k-3] + fft_outputbuf[k+3]+fft_outputbuf[k+4])/4);
sumofRatio += Ratio;
}
Draw_FFT_Figure(); // 每搜索一个频点,绘制一次频谱图
printf("Avg Ratio %.1lf ", sumofRatio/10);
printf(" SumofOverOne %.1lf",SumofOverOne*1.0/10);
printf(" Possibility %.1lf\n", sumofRatio/10*1+SumofOverOne*1.0/10*5);
Possibilities[k] = sumofRatio/10*1+SumofOverOne*1.0/10*5;
k++;
sweepfre += 500000;
if(sweepfre + 70000 + 100 >= UPFRE + 500000) // 一轮扫频结束
{
double max=0;
int mark=0;
for(int i=0;i<SIZE;i++) //遍历Possibilities数组,找到最大的
{
if(max < Possibilities[i])
{
max = Possibilities[i];
mark = i;
}
}
printf("Max Possibility = %.1lf ",max );
printf("Locked Fre %.1lf\n Now Fine Tuning...", 10+0.5*mark);
int fre = (10+0.5*mark)*1000000 - 70000 ;
// 10M的时候DDS实际频率 9929900 20M的时候19930000
// 使用边界搜索的方式获得让中心频率为70.2KHz的本振频点
int serachlow = fre - 1000;
int serachup = fre + 1000;
for(int serachfre=serachlow;serachfre<=serachup;serachfre+=100)
{
Freq_Amp_set(serachfre, 600);
printf("Now DDS Fre %d\n", serachfre);
Sample_FFT(0,0);
double maxmag = 0;
for(int i=50;i<650;i++)
if(maxmag < fft_outputbuf[i])
maxmag = fft_outputbuf[i]; // 获取fft的最大模值
double sumof=0;
for(int i=50;i<650;i++) // 获取fft的平均模值
sumof += fft_outputbuf[i];
double avg = sumof/600;
/* 若70.2KHz为中心频点? */
if( fft_outputbuf[351] > fft_outputbuf[350]*2 && fft_outputbuf[351] > fft_outputbuf[352]*2 && fft_outputbuf[351] > 5*avg )
{
printf("Fine Tuning Completed!!!");
printf("Actual DDS Fre %d\n", serachfre);
LCD_DispStr(100, 80, " ",&tFont16); // 显示搜索完毕
LCD_DispStr(100, 80, "Serach Completed ",&tFont16); // 显示搜索完毕
char lcd_string[50];
sprintf(lcd_string, "Carrier Frequency: %.1lf MHz", (fre+72000.0)/1000000 );
LCD_DispStr(15, 50, " ",&tFont16);
LCD_DispStr(15, 50, lcd_string,&tFont16);
isLocked = 1;
return fre;
}
}
sweepfre = 9929900; // 设为初始频率
return 0; // 退出扫频
}
printf("No Perfect point at this DDS Fre\n");
}
return 0;
}AM、FM 解调原理的分析与计算
这一部分偏理论分析,主要分析如何从理论上判断调制方式,Ma的计算,Mf的计算。
我会用Matlab仿真来辅助讲解分析
AM调制原理和Ma调幅度的计算*
AM调制是使载波的幅值随调制信号的大小变化而变化, 而频率保持不变的调制方式。Ma反应了载波幅值的变化量与调制信号大小的变化量的关系。

clear
fc=1000; %载波信号频率
fm=20; %调制信号频率
Fs=4000; %采样频率
t = 0:0.001:0.5;
A0 = 1;
A1 = 0.8; % 调幅度
w0=2*fc*pi;
w1=2*fm*pi;
Uc=A0*cos(w0*t); %载波信号
mes=1+A1*cos(w1*t); %调制信号
subplot(3,1,1);
plot(t,mes);
title('载波信号');
Uam=modulate(mes,fc,Fs,'am'); %AM已调信号
subplot(3,1,2);
plot(t,Uam);
title('AM调制后的信号');
C3=fft(Uam); %对已调信号进行傅里叶变换
asd=abs(C3); % 求模
subplot(3,1,3);
plot(asd);
title('AM信号FFT结果');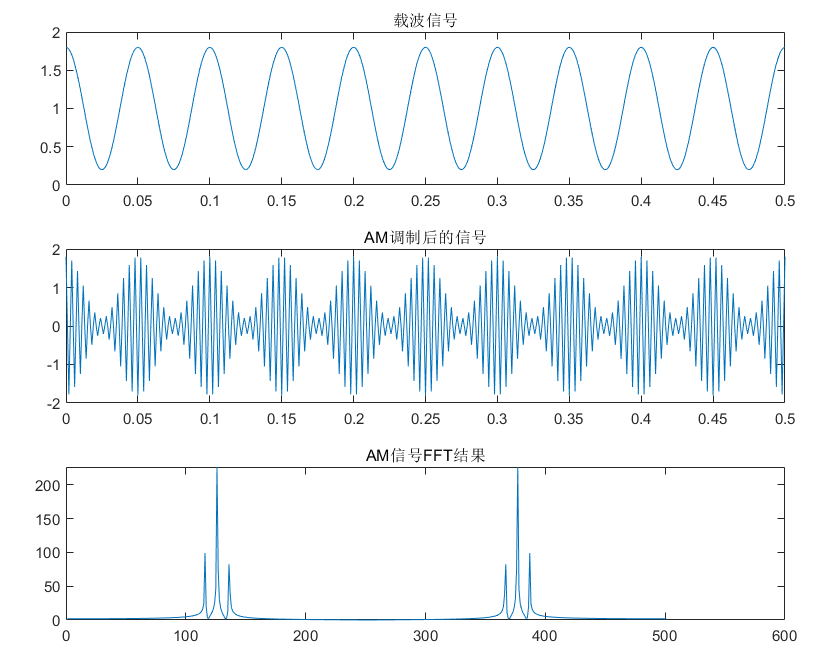
这里用Matlab对AM调制信号进行仿真,可以看到,经过AM调制后信号的包络就是原先的信号。
而从FFT的结果可以看出,AM调制后的信号有三条谱线(这里显示的是FFT的原始结果,没经过平移,所以右侧也有一个对称的形状,我们只看一侧)。
中间的是中心频率对应的幅值,左右两侧距中心的的频率偏移正好为载波的频率。左右谱线与中间谱线的幅值关系,反应了调幅度。
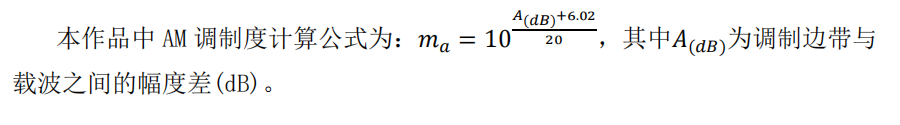
比如就以这个为例子,左侧的幅值为99,右侧的幅值为82,取均值90.5, 中间幅值226,A(dB) = 20*log10(90.5/226)=-7.95,Ma=10^((-7.95+6.02)/20)=0.801
算出来与我们设定的调频度0.8非常接近。
下面是C语言的AM分析源码。
/* AM分析 此时的中心频点已经通过DDS微调的方式锁定在了70.2KHz 返回Ma*/
double AM_FFTAnalyze()
{
Sample_FFT(0,0); // ADC采样并做FFT 不打印任何调试信息
double sumof = 0;
for(int i=50;i <= 650;i++)
sumof += fft_outputbuf[i];
double avg = sumof / 600; // 计算数组平均值
int i=0;
double Th = 6;
for( i=402;i>351;i--) // 找AM的频点,从右侧80.4K处找起,一直到70.2KHz
{
if(fft_outputbuf[i] / avg > Th && fft_outputbuf[i] > fft_outputbuf[i+1] && fft_outputbuf[i] > fft_outputbuf[i-1] )
{
printf("Find Right Point at %.1lfKHz \n", i*200.0/1000); // 找到了频点
int fre = abs((i-351)*200); //如果距离中心频点小于1KZ的话,需要重新找
if( fre < 1000 )
{
i=402;
Th -= 1;
continue;
}
else
{
printf("Tuning Fre %d\n", fre); // 间隔即为载波频率
Global_DAC_Fre = fre;
break;
}
}
}
double Max = (fft_outputbuf[351] + fft_outputbuf[350] + fft_outputbuf[352])/3 , Mup, Mlow;
Mup = (fft_outputbuf[i] + fft_outputbuf[i+1] + fft_outputbuf[i-1])/3 ; // 右边频幅值
Mlow = (fft_outputbuf[351 - (i-351)]+fft_outputbuf[352 - (i-351)]+fft_outputbuf[350 - (i-351)])/3; // 左边频幅值
double dB = 20*log10((Mup+Mlow)/2/Max);
double M_th = pow(10, (dB+6.02)/20); // 带入公式计算 M_th 是计算结果,结果在0~1之间 M_ac是之前修正的计算方法,现在已经弃用
double M_ac = 33.19*M_th*M_th*M_th + (-34.39)*M_th*M_th + 91.21*M_th + -0.08307;
printf("Ma %.3lf\n", M_th);
if( M_th >= 0.1 && M_th <= 1.1 )
{
char lcd_string[50];
sprintf(lcd_string, "Ma: %.3lf Modulated Fre %.2lf KHz", M_th, Global_DAC_Fre*1.0/1000 );
LCD_DispStr(300, 35, " ",&tFont16);
LCD_DispStr(300, 35, lcd_string,&tFont16);
return M_th;
}
return 0.01;
}FM调制原理和Mf调频度的计算*
FM 调频是使载波的频率随调制信号的大小变化而变化,而振幅保持不变的调制方式。因为已调信号反映出载波矢量角度上的变化,所以又被称为调角(这里要重点区分一下FM与PM之间的联系与区别)。
这里最重要的一点是基带信号与瞬时频率偏移成线性对应关系 。即瞬时频率偏移等于基带信号的线性放大,通过这句话可以直接确定瞬时频率偏移与基带信号的关系,进而确定最终调制之后信号的表达式。
那么首先以余弦信号的调制解调过程来讲解并且扩展到一般信号中去:
这里的Mf被称为调频灵敏度,是FM中最常出现的一个量,调频灵敏度说白了就是一个收缩因子,这个因子主要作用是线性控制调制信号所引起的瞬时频率偏移。
有了公式,我们用Matlab生成FM调制信号,然后对其进行FFT分析。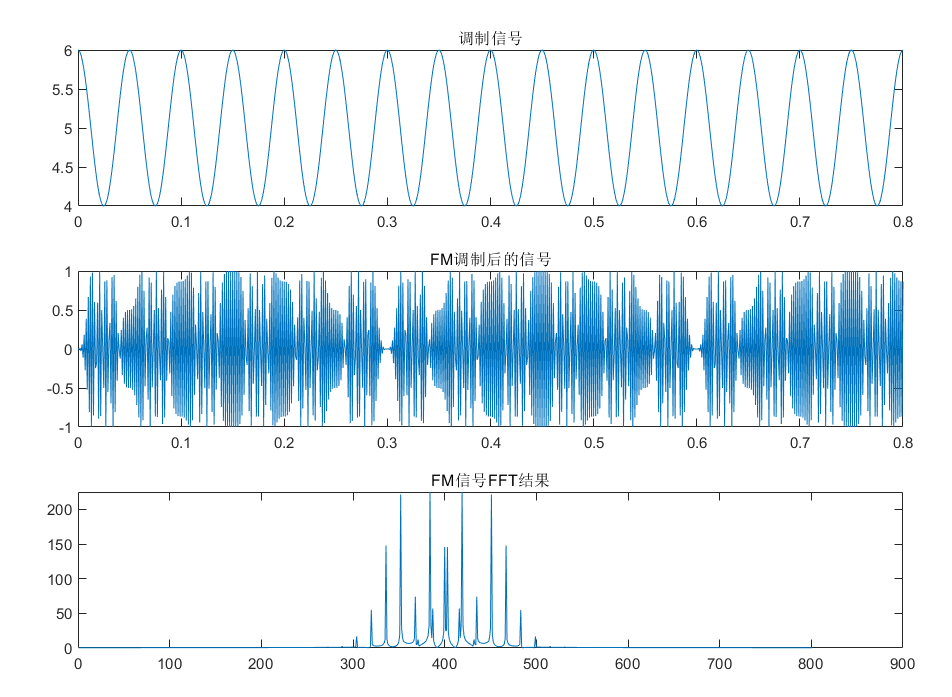
如何计算Mf(重点)**
那么,有了这些东西,我们该怎么计算Mf呢?毕竟这里可不像Ma一样,用一条公式就告诉了我们Ma和三条谱线幅值比例的关系。
有人会说,不就是拿最大频偏除以载波频率吗?
问题是,最大频偏其实很难通过FFT的结果判断出来,因为很难看出频率偏移是在哪里截止的,特别是Mf不为整数的情况下。
所以我们需要从数学上入手,找到一个根据幅值之间的关系,反推回Mf的算法。
这个算法是我的电赛指导老师告诉我的,运用了模式匹配的思想。跟其他的算法相比,准确度和计算速度有了很大的提升。
简单来说,就是先建立一个Mf的值与各边频之间幅值之比的表,我们称之为理论表。
例如,在Mf=1的情况下 J1/J0=0.31,J2/J1 = 0.02,J3/J2 = 0.0005
在Mf = 2的情况下 J1/J0=6.02,J2/J1 = 2.19,J3/J2 = 0.28
然后对于一个FM信号的FFT频谱,我们计算出它的各边频幅值之间的比值,并跟前面的理论表中的值进行比对,取出差距最小的那个值,这个值对应的Mf就是我们的计算结果。
下面是Matlab的仿真代码结果,告诉了我们这种方法的理论差值,可以看到,除了部分区间,其他的计算结果非常接近真实值。
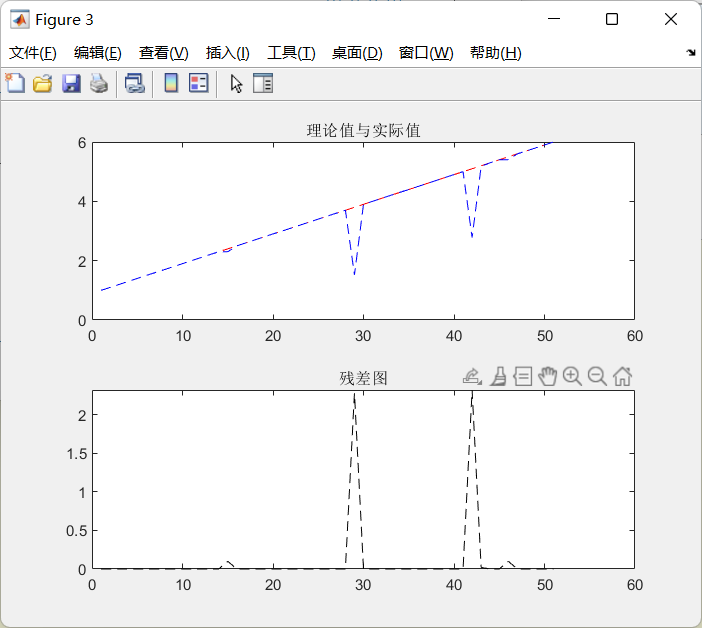
下面是Matlab理论仿真的代码
clear all;
close all;
%% 生成mf数组
rata1 = zeros(301,1);
rata2 = zeros(301,1);
rata3 = zeros(301,1);
rata4 = zeros(301,1);
rata5 = zeros(301,1);
rata6 = zeros(301,1);
i = 1;
for z = 0:0.02:6
rata1(i) = (besselj(1,z)/besselj(0,z))^2;
rata2(i) = (besselj(2,z)/besselj(0,z))^2;
rata3(i) = (besselj(3,z)/besselj(0,z))^2;
rata4(i) = (besselj(4,z)/besselj(0,z))^2;
rata5(i) = (besselj(5,z)/besselj(0,z))^2;
rata6(i) = (besselj(6,z)/besselj(0,z))^2;
i = i + 1;
end
rela_form = [rata1,rata2,rata3,rata4,rata5,rata6];
tt=1:0.1:6;
length_1=size(tt);
mf_find_copare=zeros(2,length_1(2));
kk=1;
for mf=1:0.1:6
%% 产生fm信号
fmod = 10e3; % 调制信号频率(Hz)
Amp = 1; % 调制信号幅度
fc = 70e3; % 载波频率(Hz)
Ac = 6; % 载波幅度
% mf = 1.2; % 调频指数
%
kf = mf * 2 * pi * fmod / Amp
diatf = kf * Amp
B = 2 * (mf + 1) * fmod
%
fs = 819200; % 采样率
N = 4096; % 样点总数
t = (0:N-1)'/fs; % 时间t
%绘制时域波形
m_t = Amp*sin(2*pi*fmod*t); % 调制信号
phi_t = kf*cumsum(m_t)/fs; % 相位积分
s_t = cos(2*pi*fc*t + phi_t); % 已调信号\
% figure(1)
% subplot(1,3,1)
% plot(t, s_t , 'b'); % 绘波形
% xlabel('time');
% ylabel('amplitude');
% title('时域波形');
% %绘制功率谱
% L = length(s_t); % 取得序列长度
% u = fftshift(fft(s_t )); % 离散傅⾥叶变换,求频谱
% u_pow = pow2db(abs(u).^2); % 幅度转为dB
% w = (0:L-1)'*fs/L - 1/2*fs; % 横坐标-频率
% subplot(1,3,2);
% plot(w, u_pow);
% grid on;
% xlabel('frequency(Hz)');
% ylabel('magnitude(dB)');
% title('功率谱');
% %% 解调
% %fortly
% [lpf_b,lpf_a] = butter(3, (fc/5)/(fs/2)); % 设计低通滤波器
% t = (0:N-1)'/fs; % 时间t
% r_t = s_t;
% subplot(1,3,3)
% r_d_t = [0;diff(r_t)]; % 求微分
% r_e_t = abs(r_d_t); % 包络检波
% demod_t = filter(lpf_b, lpf_a, r_e_t); % 滤波
% plot(t, demod_t , 'b'); % 绘图
% title('解调波形');
%% 峰值提取
s_t = awgn(s_t,30,'measured');
FFT_Fm=abs(fft(s_t,4096));
Input_Amp=FFT_Fm;
figure(2)
subplot(2,1,1)
plot(Input_Amp);
subplot(2,1,2)
plot(FFT_Fm);
Amp1=zeros(2048,1);
Amp2=Amp1;
Amp3=Input_Amp;
Amp_find_cnt=0;
Amp_find_index=zeros(1,50);
Wave_type=0;
for i=1:2048
if Input_Amp(i)<0.01*1000
Amp1(i)=0.01*1000;
else
Amp1(i)=Input_Amp(i);
end
end
Amp3(1)=0;Amp3(2)=0;
for i=3:2048
if Amp1(i)/Amp1(i-2)>5
Amp2(i)=1;
else
Amp2(i)=0;
Amp3(i)=0;
end
end
Amp_find_cnt=0;
for i=2:2047
if Amp3(i)>=Amp3(i-1) && Amp3(i)>Amp3(i+1)
Amp_find_cnt=Amp_find_cnt+1;
Amp_find_index(1,Amp_find_cnt)=i;
end
end
Amp_find_cnt
Amp_find_index(1,1:Amp_find_cnt)
if Amp_find_cnt==1
Wave_type=0;
elseif Amp_find_cnt==3
Wave_type=1;
Am_index=Amp3(1,Amp_find_index(2))/Amp3(1,Amp_find_index(1))%需要替换
else
Wave_type=2;
fc_cal=round(fc*N/fs);% fc*4096/819200
for i=1:Amp_find_cnt
if Amp_find_index(i)>= (fc_cal-2)&& Amp_find_index(i)<=(fc_cal+2) % 70kHz中频
Amp_find_index(i)
J0=Amp3(Amp_find_index(i))^2
J1_J0=Amp3(Amp_find_index(i-1))^2/J0;
if i>2
J2_J0=Amp3(Amp_find_index(i-2))^2/J0;
else
J2_J0=0;
end
if i>3
J3_J0=Amp3(Amp_find_index(i-3))^2/J0;
else
J3_J0=0;
end
if i>4
J4_J0=Amp3(Amp_find_index(i-4))^2/J0;
else
J4_J0=0;
end
if i>5
J5_J0=Amp3(Amp_find_index(i-5))^2/J0;
else
J5_J0=0;
end
if i>6
J6_J0=Amp3(Amp_find_index(i-6))^2/J0;
else
J6_J0=0;
end
break;
end
end
end
mindelta = 65535;
i=1;
length=size(rela_form);
for i = 1:length(1)
distence = (J1_J0-rela_form(i,1))^2+(J2_J0-rela_form(i,2))^2+(J3_J0-rela_form(i,3))^2+(J4_J0-rela_form(i,4))^2;
% distence = abs(J1_J0-rela_form(i,1))+abs(J2_J0-rela_form(i,2))+abs(J3_J0-rela_form(i,3))+abs(J4_J0-rela_form(i,4))+abs(J5_J0-rela_form(i,5))+abs(J6_J0-rela_form(i,6));
if distence <= mindelta
mindelta = distence;
mf_find=(i-1)*0.02;
end
end
mf_find_copare(1,kk)=mf;
mf_find_copare(2,kk)=mf_find;
mf
mf_find
kk=kk+1;
end
figure(3)
subplot(2,1,1)
plot(mf_find_copare(1,:),'--r')
title('理论值与实际值')
hold on
plot(mf_find_copare(2,:),'--b')
subplot(2,1,2)
plot(mf_find_copare(1,:)-mf_find_copare(2,:),'--k')
title('残差图')下面是C语言FM分析的源码。
/* FFT分析FM频谱获得Mf 此时中心频点已经通过DDS微调锁定在了70.2KHz 返回Mf */
double FM_FFTAnalyze(void)
{
Sample_FFT(0,0);
double sumof = 0;
for(int i=50;i <= 650;i++) // 计算均值
sumof += fft_outputbuf[i];
double avg = sumof / 600 ;
double J[10] = {0}; // 储存基频,左第一边带,左第二边带,......的幅值
double F[10] = {0};
int peaks=0;
int mark1=0, mark2=0;
for(int i=350;i<650;i++)
{
if(fft_outputbuf[i] > fft_outputbuf[i+1]*2 && fft_outputbuf[i]*2 > fft_outputbuf[i-1] && fft_outputbuf[i] > 5*avg ) // 寻峰算法,存入J中
{
J[peaks] = fft_outputbuf[i];
F[peaks] = i;
printf("At %.1lf KHz find %d Peak Magnitude %.1lf \n", i*200.0/1000, peaks, fft_outputbuf[i] );
peaks++;
}
}
int Diff[10];
int serachfor = 100;
for(int i=0;i<peaks-1;i++)
{
Diff[i] = F[i+1] - F[i];
}
for(int i=0;i<peaks-1;i++) // 从小到大排序
for(int j=i+1;j<peaks-1;j++)
if(Diff[i] > Diff[j])
{
unsigned short temp;
temp = Diff[i];
Diff[i] = Diff[j];
Diff[j] = temp;
}
for(int i=0;i<peaks-1;i++)
{
if( Diff[i] != 1 && Diff[i] < 500)
{
serachfor = Diff[i];
break;
}
}
printf("\n Min gap fre: %d \n", serachfor*200);
J[0] = (fft_outputbuf[351]+fft_outputbuf[350]+fft_outputbuf[352])/3 ;
J[1] = (fft_outputbuf[351+ (serachfor)]+ fft_outputbuf[350+ (serachfor)] + fft_outputbuf[352+ (serachfor)])/3 ;
J[2] = (fft_outputbuf[351+ (serachfor)*2]+ fft_outputbuf[351+ (serachfor)*2] + fft_outputbuf[351+ (serachfor)*2])/3;
J[3] = (fft_outputbuf[351+ (serachfor)*3] + fft_outputbuf[351+ (serachfor)*3] + fft_outputbuf[351+ (serachfor)*3])/3;
J[4] = (fft_outputbuf[351+ (serachfor)*4] + fft_outputbuf[351+ (serachfor)*4] + fft_outputbuf[351+ (serachfor)*4])/3;
Global_DAC_Fre = serachfor*200;
printf("Tuning Fre %.1lfKHz \n", Global_DAC_Fre*1.0/1000);
double J1_J0 = J[1]/J[0], J2_J0 = J[2]/J[0], J3_J0 = J[3]/J[0], J4_J0 = J[4]/J[0]; // 计算出J1/J0 J2/J0 ....等值
double Min = 65535;
int mark = 0;
for(int i=0;i<301;i++)
{
// 与标准贝塞尔函数比值计算欧几里得距离,最近的即为最佳匹配
double O_dis = (J1_J0-J_Table[i][0])*(J1_J0-J_Table[i][0]) + (J2_J0-J_Table[i][1])*(J1_J0-J_Table[i][1]) + (J3_J0-J_Table[i][2])*(J3_J0-J_Table[i][2]) + (J4_J0-J_Table[i][3])*(J4_J0-J_Table[i][3]);
if(O_dis < Min)
{
Min = O_dis;
//printf("Mf = %.1lf\n", (i-1)*0.02);
mark = i;
}
}
double Mf = (mark-1)*0.02;
printf("Result Mf = %.3lf\n",Mf);
if(Mf > 3.10 && Mf <= 3.14 )
Mf -= 1.32;
else if(Mf >=2.94 && Mf < 2.98 )
Mf -= 0.96;
else if(Mf >=2.76 && Mf <= 2.80 )
Mf -= 0.58;
else if(Mf >=4.48 && Mf <= 4.52 )
Mf -= 0.9;
else if(Mf >=1.50 && Mf <= 1.54 )
Mf += 2.28;
else if(Mf >=4.56 && Mf <= 4.74 )
Mf -= 0.44;
else if(Mf >=5.18 && Mf <= 5.28 )
Mf += 0.30;
else if(Mf >=1.22 && Mf <= 1.26 )
Mf -= 0.20;
printf("Fixed Mf %.3lf\n", Mf);
char lcd_string[50];
sprintf(lcd_string, "Mf: %.3lf Carrier Fre %.1lf Max Fre Offset %.3lf", Mf, Global_DAC_Fre*1.0/1000, Mf*Global_DAC_Fre*1.0/1000);
LCD_DispStr(300, 35, " ",&tFont16);
LCD_DispStr(300, 35, lcd_string,&tFont16);
return (mark-1)*0.02;
}判断调制类型
有了上面这些内容,判断调制类型就很简单了,简单来说就是数谱线的个数,未调制的时候一条谱线,AM调制的时候3条谱线,FM调制的时候至少5条以上谱线。
/* 通过FFT判断是AM还是FM */
int AM_FM_Detect()
{
int sumofPoint=0;
for(int i=0;i<10;i++)
{
Sample_FFT(0, 0);
double sumof = 0;
for(int i=50;i <= 650;i++) // 计算FFT均值
sumof += fft_outputbuf[i];
double avg = sumof/ 600;
printf("Avg %.3f\n", avg);
int count = 0;
for(int i=55; i<= 650;i++) // 数频点的个数
{
if(fft_outputbuf[i] > fft_outputbuf[i+1] && fft_outputbuf[i] > fft_outputbuf[i-1] && fft_outputbuf[i] > avg * 5 )
count++;
}
sumofPoint += count;
}
printf("Avg Point %.1lf\n", sumofPoint*1.0/10);
if(sumofPoint*1.0/10 > 4.5) // 若均大于4.5,则认为是FM
{
printf("Is FM\n");
return FM;
}
else // 若均值小于4.5,则认为是AM
{
return AM;
}
return 0;
}软件上的改进措施
ADC采样与FFT
ADC只采4000个点,剩余96个点用0补齐,这样就能避免采样率对不上的问题。或者改进ADC的时钟,使其为2的次幂(比较不可行,因为时钟树牵一发而动全身)。
改进频点判断算法
改进判断频点的Possibility算法,让误判断的概率更小。
一些图片
由于实物已经被封箱了,比赛的时候也没有拍照和截图,只有一张照片。后面如果拿回来的话考虑补上。
结语
这次比赛算是得到了一波经验和教训,后续继续努力吧,要学的东西还有很多。